Largest Rectangle in Histogram

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of the largest rectangle in the histogram.

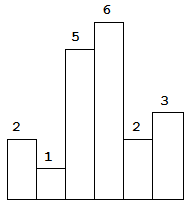
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

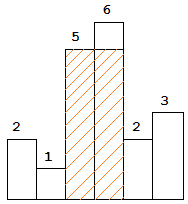
The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example, Given height = [2,1,5,6,2,3], return 10.

Hint

The point of this algorithm is to maintain a stack where higher element is always greater or equal to the lower element.

Why do we need to maintain that kind of stack? Because if we have a non-decreasing list, we can easily calculate the maximum area in one scan. We just need to compare: height[i] * (n - i) for every i.

So how do we maintain this stack?

If we keep seeing larger element, we just need to push them onto the stack. If we see a smaller (compared to the top element on the stack) element, we need to do two things:

1.Pop the stack until we can maintain the non-decreasing order. Pushing the smaller element for m times, where m = number of poped elements.

2.Keep track of the maximum area that cause by those pop.

For Example.

we have height = {1,3,5,7,4}. We push onto the stack for {1,3,5,7} then we see 4. 4 is less than 7, so we need to pop. We stop popping until we see 3. However many times we pop, we push 4 onto the stack. Therefore the resulted stack would be {1,3,4,4,4}. Because of popping 7, we need to remember that the maximum area that contains 7 is 7. The largest area that contains 5, the other element which get popped, is 10. So we take that down. We then finish processing all the elements in the original array and end up with a non-decreasing stack {1,3,4,4,4}. We can compute the largest area of this stack, which is 4*3 = 12. Since 12 is larger than the previous largest, 10, we output 12.

Code (Java)

public class Solution {
    public int largestRectangleArea(int[] height) {
        int count = 0;
        int max_area = 0;
        Stack<Integer> stack = new Stack<Integer>();
        for(int i=0;i<height.length;i++){
            count = 0;
            while(!stack.isEmpty() && stack.peek() > height[i]){
                int k = stack.pop();
                count++;
                max_area = Math.max(max_area,count*k);
            }
            
            
        for(int j=0;j<=count;j++)
        stack.push(height[i]);
        }
        count = 0;
        while(!stack.isEmpty()){
            int k = stack.pop();
                count++;
                max_area = Math.max(max_area,count*k);
        }
        
        return max_area;
    }
}