Gas Station

#####There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1).You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station’s index if you can travel around the circuit once, otherwise return -1.

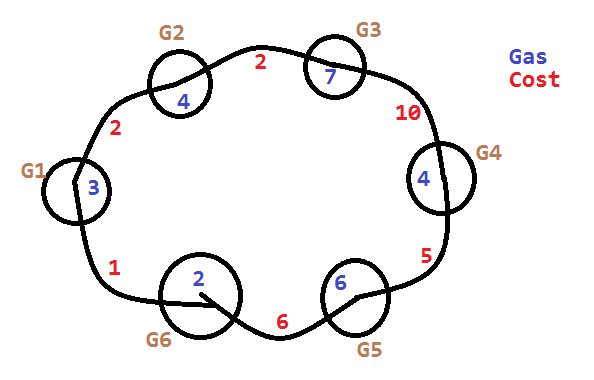
Ans = 5

Hint

lets have a simple brute force solution.

For each i(making it a start point) check if we can make a complete circular path. If such a path exist return i otherwise return -1

Time Complexity of above algo is O(n2).

Can we reduce it to O(n)? Yes, the solution is pretty simple. There is no need to traverse the whole array for each i , as we know how much initial gas is required at last_starting_point to reach i. If we put i as starting_point and successfully reach upto last_starting_point with required gas as storage then we will be able to traverse the comple path

For Eg:

gas[i] = {3,4,7,4,6,2} and cost[i] = {2,2,10,5,6,1}, let suppose we start at station 1 with empty tank. we will reach station 2 with gas storage 1 (3-2). next we will reach station 3 with gas storage 10 (4+1 - 2). Next reach station 4 with storage 0 (10-10). Now we can’t move further as gas remaining is 4 while required is 5. if we have initial gas storage as 1 at station 1 we will be able to able to succesfully reach station 4 . So now we mmove start point as station 4 and from station 4 if will successfully able to reach station 1 with gas required 1 we will be able to complete one circle. Conclusion: we just need to maintain the gas required as initial_gas_storage_required and at i==n if curr_gas_store >= initial_gas_storage_required we will return last start point otherwise -1.

Code (Java)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
    
    int n=gas.length;
    int gasRequiredAtZero=0;
    int start =0,storage=0;
    for(int i=0;i<n;i++){
        storage = storage+gas[i]-cost[i];
        if(storage<0){
            start=(i+1)%n;
            gasRequiredAtZero+=storage * -1;
            storage=0;
        }
    }
    if(storage>=(gasRequiredAtZero))
        return start;
    else
        return -1;
    }
}